暑假看了一些书,因此随手记录一下所学所想。
先从具体数学开始吧,由于博主只是个大一的本科生,数学基础并不扎实,欢迎指正错误。
本篇主要涉及具体数学第一章的内容,以及我对其中一些内容的拓展。
汉诺塔问题
开篇引入的就是很多人都熟知的问题,问题的介绍就不再赘述了。
设三根柱子分别为\(A,B,C\),目标是将\(n\)个圆盘从柱子\(A\)移动到柱子\(C\)上,并记有\(n\)个圆盘的汉诺塔问题的最优解为\(T_n\),先考虑构造一个可行的方案:
将前\(n-1\)个小的圆盘移动至\(B\),再将最大的圆盘移动至\(C\),最后将\(n-1\)个圆盘移动至\(C\)。
这是一个可行的方案,因此对最优解\(T_n\),有\(T_n\leq 2T_{n-1}+1,\forall n\in\mathbb{N^+}\)。
书中随后证明了所有可行解的次数都大于等于\(2T_{n-1}+1\),因此可以断言这是一个最优解。
由此受到启发,可以抽象出一个证明某个解是最优解的思路:先证明该解是可行解,再证明所有的可行解都不会比该解更优。
直线分割平面问题
这个问题是高中数学的经典问题,但还可以从不同角度去探讨这个问题的解。
记最优解为\(L_n\),先引入平面图欧拉公式:\(V-E+F=2\),其中\(V,E,F\)分别为顶点数,边数,区域数。注意欧拉公式中的边数不是直线数。
第\(n\)条直线可以至多形成\(n\)个交点,考虑在平面上构造一个充分大的圆,使得所有的交点都在圆内,并与每条直线都有两个交点,共形成\(2n\)个交点。
将新形成的交点中在圆上相邻的点对用线段连接,形成\(2n\)条边,得到一个凸多边形。再删去圆和所有直线在凸多边形外的部分,此时这个凸多边形内部的区域数即\(L_n\)。
从而,平面上的点数\(V=\frac{n(n-1)}{2}+2n=\frac{n^2+3n}{2}\)。原先的每条直线被\(n+1\)个点分割为\(n\)条边,则边数\(E=n\cdot n+2n=n^2+2n\)。
又由凸多边形外也是一个区域,代入平面图欧拉公式得\(V-E+L_n+1=2\),即\(L_n=\frac{n(n+1)}{2}+1\)。
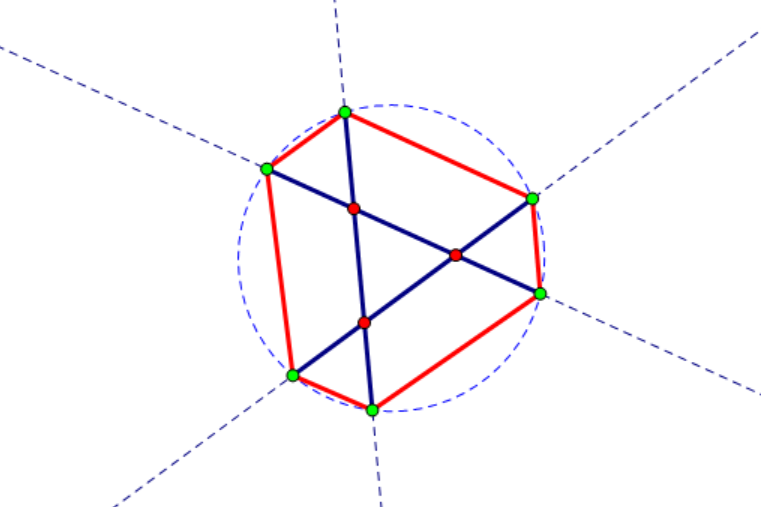
下图是\(n=3\)时的一个例子,其中绿色的点和红色的边分别为新形成的点和新形成的边。
约瑟夫问题
这个问题引申出来的内容就多一些了,并且我用线性空间对递推式的封闭形式进行了讨论。先规定\(n\)为人数,数到第\(m\)个人被选中,\(J(n)\)为幸存者的编号,\(\%\)为取模运算。
\(m=2\)的情形
书中先讨论的是\(m=2\)的情形,求解的方法是先选到只剩下\(\left\lfloor \frac{n}{2}\right\rfloor\)个人,将问题转换成\(\left\lfloor \frac{n}{2}\right\rfloor\)个人的情形。
由此受到启发,可以抽象出一些求递归式的问题的解法:先对问题进行有限步的处理,构造一个到\(n\)更小的情形的单射,从而得到递归式。
例如在该问题中,先进行报数,剩下\(\left\lfloor \frac{n}{2}\right\rfloor\)个人以 \[ f(x) =\begin{cases}\frac{x-1}{2},&\text{$n$ is odd}\\\frac{x+1}{2},&\text{$n$ is even}\end{cases} \] 的方式进行重新编号,很显然这是一个单射,因此有逆映射 \[ f^{-1}(x) =\begin{cases}2x+1,&\text{$n$ is odd}\\2x-1,&\text{$n$ is even}\end{cases} \] 此时即可转换为人数为\(\left\lfloor \frac{n}{2}\right\rfloor\)时的情形,幸存者编号为\(x=J(\left\lfloor \frac{n}{2}\right\rfloor)\)。则人数为\(n\)时\(J(n)=f^{-1}(x)\),整理一下即为书上的形式。
事实上,这个思路运用的非常广泛,并且通常来说最开始有限步的处理会影响到用递推式求解的复杂度。例如考虑\(m\)为任意正整数的情况:
为方便讨论,将每个人的标号记成\(0,1,2,...,n-1\),先进行一轮报数,编号为\(k=(m-1)\%n\)的人被选中。构造一个映射\(f\)将编号序列\(k,k+1,...,n-1,0,1,2,...,k-2\)映射为\(0,1,2,...,n-2\),转换为\(n-1\)的情形。很显然\(f\)是一个双射,并且有\(f^{-1}(x)=(x+k)\%n\),从而有 \[ J(n)=(J(n-1)+(m-1)\%n)\%n\tag{1}\label{Equ:1} \] 利用\(\eqref{Equ:1}\)计算\(J(n)\)的时间复杂度为\(O(N)\),而利用书中的公式计算的时间复杂度为\(O(\log N)\),在最开始有限步的处理确实影响到了利用递推式求解的复杂度。
利用线性空间求递推式的封闭形式
书中给出\(m=2\)时的封闭形式和二进制下的形式,这里不再赘述。
而书中提到了利用独立的特解求形如 \[ f(j)=a_j,1\leq j<d\\ f(dn+j)=cf(n)+b_j,0\leq j<d,n\geq1\tag{2}\label{Equ:2} \] 的递归式的封闭形式的方法,称为成套方法(repertoire method),并且提到有多少个独立的参数就需要多少个独立的特解,却并没有剖析其背后的原因。事实上,可以从线性空间的角度来看待这个问题。
给定\(c,d\),所有以\(\eqref{Equ:2}\)形式定义的函数 \(f\)构成的集合\(V\)不是空集。易验证\(V\)在函数的加法和函数与实数域\(\mathbb{R}\)的纯量乘法下构成域\(\mathbb{R}\)上的线性空间。
考虑实数域上\(2d+1\)维向量构成的线性空间\(W\),构造一个映射 \[ \sigma:W\to V\\ (a_1,...,a_{j-1},b_0,...,b_{j-1})\mapsto f \] 其中\(f\)按\(\eqref{Equ:2}\)定义,易验证\(\sigma\)是一个线性映射。
取\(W\)中的一组基\(\alpha_1=(1,0,...,0),\alpha_2=(0,1,...,0),...,\alpha_{2d+1}=(0,0,...,1)\),经\(\sigma\)映射成\(f_1,...,f_{2d+1}\)。
设\(g(x)=\sum_{i=1}^{2d+1}k_if_i\)为零函数,即\(g(x)=0,\forall x\in\mathbb{N^+}\)。
注意到 \[ f_i(j)=\begin{cases}1,i=j\\0,i\neq j\end{cases}\textbf{ $,\forall i,j\in\{1,2,...,2d+1\}$} \] 则\(\forall i\in\{1,2,...,2d+1\},g(i)=k_if_i(i)=k_i=0\),即\(f_1,...,f_{2d+1}\)线性无关。
又对任意按\(\eqref{Equ:2}\)定义的\(f\),有\(f=a_1f_1+...+a_{j-1}f_{j-1}+b_0f_j+...+b_{j-1}f_{2d+1}\)。
由此,\(f_1,...,f_{2d+1}\)为\(V\)的一组基,则\(\sigma\)是一个双射,即\(\sigma\)是一个可逆线性映射。
则 \[ \begin{align*} f&=\sigma^{-1}((a_1,...,a_{j-1},b_0,...,b_{j-1}))\\ &=\sigma^{-1}(\sum_{i=1}^{j-1}a_i\alpha_i+\sum_{i=0}^{j-1}b_i\alpha_{i+j})\\ &=\sum_{i=1}^{j-1}a_i\sigma^{-1}(\alpha_i)+\sum_{i=0}^{j-1}b_i\sigma^{-1}(\alpha_{i+j})\\ &=\sum_{i=1}^{j-1}a_if_i+\sum_{i=0}^{j-1}b_if_{i+j} \end{align*} \] 因此,成套方法的本质即取\(W\)的一组基,解出\(V\)的一组基\(f_1,...,f_{2d+1}\),从而得到\(f\)的封闭形式。