这个专题记录一些讨论班的内容。这一部分可视化目前有三章内容,最初的动机是讨论Lax上的三个对偶变分问题的几何意义。这一章主要是支撑函数的几何意义以及引出局部凸空间上闭凸子集和连续线性泛函的紧密联系,并给出了一些应用。
如未特殊说明,默认所有讨论在\(\mathbb R\)上的赋范线性空间\(X\)及其对偶空间\(X^*\)上进行。下面是一些记号和前置知识。
对\(l\in X^*\),记其导出的开半平面\(H(l,c):=\set{x\in X\colon l(x)<c}\),闭半平面\(\overline{H}(l,c):=\set{x\in X\colon l(x)\leq c}\),超平面\(P(l,c):=\set{x\in X\colon l(x)=c}\)。特别地,当\(c=+\infty\)时,\(H(l,c)=\overline H(l,c)=X\);\(c=-\infty\)时,\(H(l,c)=\overline H(l,c)=\emptyset\)。 对\(x\in X\),记其半径为\(R\)的开球为\(B(x,R)\)。
Definition 1(支撑函数) 设\(M\subset X\),则\(M\)上的支撑函数为 \[ \begin{align*} S_M\colon X^*&\longrightarrow\mathbb R\\ l&\longmapsto\sup_{x\in M}l(x). \end{align*} \] 原文Ch 8 Thm 17为
Theorem 1(原文Ch 8 Thm 17) 对任一\(x\in X\),\(x\)在\(M\)的闭凸包中当且仅当\[l(x)\leq S_M(l),\forall l\in X^*.\]
支撑函数的一个动机
在Theorem 1和原文Ch 12 Thm 2中都重复证明了一个关于闭凸集的引理:
Lemma 1 设\(K\)是\(X\)的一个非空闭凸子集,则对任一\(z\notin K\),都存在\(l\in X^*\)和常数\(c\),使得\(l(z)>c\)且\(K\subset\overline H(l, c)\)。
在此之前,先回顾一下超平面分离定理。
Theorem 2(超平面分离定理) 设\(K\)是\(X\)的一个非空开凸子集,则对任一\(z\notin K\),都存在\(l\in X^*\),使得\(K\subset H(l, l(z))\)。
在该定理的记号下,我们令\(\set{A_\alpha}\)是所有包含了\(K\)的开半平面的集合,一个显而易见的结论是 \[ K=\bigcap_\alpha A_\alpha. \] 同样地,对于闭凸子集,由Lemma 1可以得到类似的结论:令\(\set{B_\alpha}\)是所有包含了\(K\)的闭半平面的集合,则 \[ K=\bigcap_\alpha B_\alpha. \] 这两个结论说明闭(开)凸集一定能写成一族闭(开)半平面的交。另外,在一个闭凸子集\(C\)上,固定一个有界线性泛函\(l\),一定存在闭半平面\(\overline H(l,c)\)包含\(C\),且\(\forall\varepsilon>0\),\(\overline H(l,c-\varepsilon)\)不包含\(C\)。这说明这个平面是紧贴着\(C\)的一个平面,不妨称其为\(C\)的支撑半平面,则定义支撑函数的一个动机就非常明显了(只需要注意到\(l\)导出的支撑闭半平面是\(\overline H\left(l,S_C(l)\right)\))。
事实上,结合前面的讨论我们已经得到了Theorem 1的一个等价形式
Theorem 3 设\(K\)是\(X\)的一个非空闭凸子集,则 \[ K=\bigcap_{l\in X^*}\overline H\left(l, S_K(l)\right). \] Theorem 1是支撑函数的一个重要应用,而这一定理从几何角度刻画了Theorem 1。该定理说明闭凸子集总能写成一族连续线性泛函导出的闭半平面的交。反之,连续线性泛函导出的闭半平面的交一定是闭凸子集。这揭示了连续线性泛函和闭凸子集的紧密联系,更一般的结果将在下一节中展示。
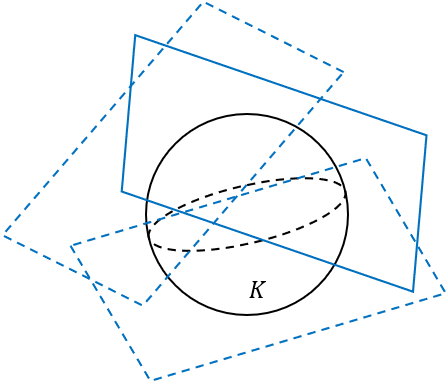
正如上图所示,Theorem 3的几何意义即闭凸子集\(K\)是所有支撑半平面(蓝色的超平面的下方)的交集。那么,Theorem 1表示的就是\(x\)在闭凸子集\(K\)中当且仅当\(x\)在所有支撑半平面内。
最后,补上Lemma 1的证明。
- Proof 由于\(K\)是闭的,则一定存在开球\(B(z,R)\)与\(K\)不交。由广义超平面分离定理,存在\(l\in X^*\)和常数\(c\),使得\(\forall u\in K,v\in B(z,R)\),都有 \[ l(u)\leq c\leq l(v). \] 而\(B(z,R)\)中的点形如\(v=z+Rx,\lVert x\rVert<1\),则有\(l(z)+Rl(x)\geq c\),即\(l(z)\geq c - Rl(x)\)。根据泛函范数定义,有 \[ l(z)\geq c-R\inf_{\lVert x\rVert < 1}l(x)=c-R(-\lVert l\rVert)=c+R\lVert l\rVert>c. \] 又由于\(l(u)\leq c,\forall u\in K\),有\(K\subset H(l,c)\),引理证毕。
LCS上的支撑与闭凸子集
记局部凸空间\(\mathscr X\)上的所有连续线性泛函为\(\mathscr X^*\),这里沿用Lax的定义,默认讨论的是Hausdorff局部凸空间。根据原文Ch 13 Thm 2':我们还需要熟知两个结论:当\(l\)是连续线性泛函时,它导出的开(闭)半平面一定是开(闭)的;在给定的拓扑下,\(\mathscr X^*\)构成线性空间。
Theorem 4(原文Ch 13 Thm 2') 设\(K\)是局部凸空间\(\mathscr X\)上的一个闭凸子集,\(z\notin\mathscr X\),则存在\(\mathscr X\)上的连续线性泛函\(l\),使得\(l(z)>c\)且\(K\subset\overline H(l, c)\)。
和上一节的讨论一样,根据Theorem 4。我们可以得到Theorem 1和Theorem 3在LCS上的版本:
Theorem 5 设\(K\)是局部凸空间\(\mathscr X\)上的一个闭凸子集,则
\(\forall x\in\mathscr X\),\(x\in K\)当且仅当\[l(x)\leq S_M(l),\forall l\in\mathscr X^*;\]
\[ K=\bigcap_{l\in\mathscr X^*}\overline H\left(l, S_K(l)\right); \]
设\(E\)是一个凸集,则 \[ \bigcap_{l\in\mathscr X^*}\overline H\left(l, S_E(l)\right) \] 是\(E\)的闭凸包。
注意一个事实:在固定的线性空间\(V\)上,改变选取的Hausdorff局部凸拓扑,\(V\)上的连续线性泛函集合也改变了。但连续线性泛函导出的闭半平面和闭凸子集之间总是存在着Theorem 5形式的关系。因此,在局部凸空间\(\mathscr X\)上,闭凸子集总能写成一族连续线性泛函导出的闭半平面的交。这就说明,如果给线性空间\(V\)配置两个不同的Hausdorff局部凸拓扑,只要连续线性泛函空间相同,一个凸子集在两个拓扑下的闭性是相同的。一个自然地想法是,这个结果反之是否成立?
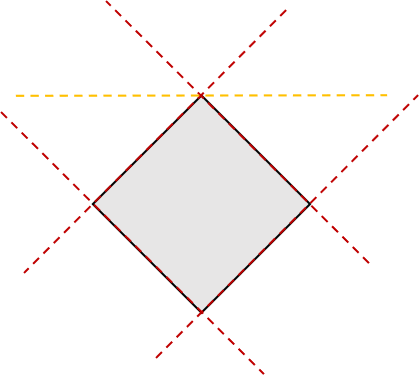
如上图所示,只需要红色的四条线对应的支撑半平面取交集就能得到里面的正方形,因此在一些闭凸子集中,有些连续线性泛函的超平面是必要的。但如果对所有闭凸子集来说,对任意一个支撑半平面\(\overline H\),都存在一个闭凸子集,在表示成支撑半平面的交时,一定需要\(\overline H\)(\(\overline H\)本身就是一个例子)。事实上,我们有如下定理
Theorem 6 设线性空间\(V\)上有两个Hausdorff局部凸拓扑\(\eta_1\)和\(\eta_2\),\((V,\eta_1)^*\)和\((V,\eta_2)^*\)是在两个拓扑下的连续线性泛函空间,\(C_1\)和\(C_2\)分别是\((V,\eta_1)\)和\((V,\eta_2)\)的所有闭凸子集,则\(C_1=C_2\)当且仅当\((V,\eta_1)^*=(V,\eta_2)^*\)。
Proof 由Theorem 5,若\((V,\eta_1)^*=(V,\eta_2)^*\),则\(C_1=C_2\)。
当\(C_1=C_2\)时,由于线性泛函\(l\)连续当且仅当\(P(l,0)\)是闭的。而\(P(l,0)\)一定是凸的,因此结合\(C_1=C_2\),有\((V,\eta_1)^*=(V,\eta_2)^*\)。
从这个定理可以看出LCS上连续线性泛函和闭凸子集的对应关系,因此在LCS上处理闭凸子集时,Theorem 5是一个非常好用的工具。
应用举例
支撑函数的简单应用
在应用支撑函数时,可以把Theorem 1看作强化版的超平面分离定理。设\(X\)是\(\mathbb R\)上赋范线性空间,\(K\)是\(X\)的一个非空闭凸子集,则对任一\(x\in X\),\(x\in X\)当且仅当\(l(x)\leq S_K(l),\forall l\in X^*\)。这蕴含了若\(x\notin X\),则存在\(l\in X^*\),使得\[l(x)>S_K(l)=\sup_{y\in K}l(k)\]这说明Theorem 1蕴含了超平面分离定理。事实上,在上一章讨论几何意义时可以看出这是非常显然的结果。
在Ch 10 Thm 6的证明中用到了支撑函数,同时原文也提到Ch 12 Thm 2和Ch 10 Thm 6是相似的。原书在证明时是利用超平面分离定理证明\(K^c\)是弱开集,从而证明\(K\)是弱闭集。如果我们考虑从闭集本身的性质出发证明,自然地,就能想到直接使用在闭凸子集的工具:Theorem 1。我们直接考虑Ch 10 Thm 6的一个更强的版本
Theorem 7 设\(K\)是\(X\)的一个凸子集,则\(K\)在弱拓扑下的闭包等于\(K\)在强拓扑下的闭包\(\overline K\)。
要从闭集本身的性质出发证明这个定理,我们只需证明\(K\)在弱拓扑下的聚点在\(\overline K\)中。
Proof 令\(K'_w\)和\(K'_s\)分别为\(K\)在弱拓扑和强拓扑下的导集,由弱拓扑弱于强拓扑易知\(K'_s\subset K'_w\)。
任给\(z\in K'_w\)和\(l\in X^*\),对任意\(\varepsilon>0\),\(\set{x\in X\colon l(x)>l(z)-\varepsilon}\)是\(z\)在弱拓扑下的一个邻域。由于\(z\)是\(K\)在弱拓扑下的聚点,存在\(y\in K\)使得\(l(y)>l(z)-\varepsilon\)。由\(\varepsilon\)任意性, \[ l(z)\leq\sup_{y\in K}l(y)=S_K(l). \] 由Theorem 1,结合\(l\)任意性,\(z\in\overline K\)。从而有\(\left(K\cup K'_w\right)\subset \left(K\cup K'_s\right)\)。
综上所述,\(K\)在弱拓扑下的闭包等于\(K\)在强拓扑下的闭包。
当然也可以用LCS的性质给出一个简短的证明:由于强拓扑和弱拓扑都是Hausdorff局部凸拓扑,且对应的连续线性泛函集合是相同的,因此由Theorem 6,对应的闭凸子集也相同。
Theorem 5的应用
Krein-Milman定理分为两部分
Theorem 8(Krein-Milman定理) \(K\)是局部凸空间\(\mathscr X\)上的非空紧凸子集,则
- \(K\)至少有一个端点;
- \(K\)是它所有端点的集合的闭凸包。
下面给出在证明了\(1\)后,\(2\)的一个证明。
Proof 由于\(\mathscr X\)是Hausdorff空间,则\(K\)一定是闭的。设\(K\)的所有端点的集合的闭凸包为\(C\),易证\(C\subset K\),从而有\(S_K(l)\geq S_C(l),\forall l\in \mathscr X^*\)。
假设\(C\neq K\),根据Theorem 5,存在\(l'\in\mathscr X^*\),使得\(S_K(l_0)> S_C(l_0)\)。由于\(K\)是紧的,\(l_0\)一定能在\(K\)上取到最大值,则\(E:=\overline H(l_0,S_K(l_0))\cap K\neq\emptyset\)。
任取\(x\in E\),若\(x\)能被表示成\(K\)中两点\(y\)和\(z\)的凸组合,由\(l_0(x)=S_K(l_0)\)和\(l_0(y),l_0(z)\leq S_K(l_0)\)(因为\(K\subset \overline H(l_0,S_K(l_0))\))得\(l_0(y_0)=l_0(z)=S_K(l_0)\),即\(y,z\in E\)。这就证明了\(E\)是极子集,并且由\(\overline H(l_0,S_K(l_0))\)和\(K\)是闭的,\(E\)也是闭的。从Lax对\(1\)的证明可以看出,\(K\)的闭极子集一定有一个\(K\)的端点\(x_0\)。又由于\(S_C(l_0)<S_K(l_0)\),\(x_0\notin C\),这与\(C\)的定义矛盾,因此\(K=C\)。
这个证明和Lax的证明本质上是一样的,但使用Theorem 5可以更好地从几何的角度去思考。