有了前两章支撑函数的几何意义、泛函范数和超平面距离之间的几何关系作为铺垫,这一章将会把原文Ch 8 Thm 7、Ch 8 Thm 7'和Ch 8 Thm 18三个对偶变分问题可视化。
记\(X^*_Y\)为\(Y\)的所有零化子,即\(X^*_Y=\{l\in X^*\colon l(y)=0,\forall y\in Y\}\)。下面是三个定理的内容。
Theorem 11(原文Ch 8 Thm 7) 设\(Y\)是\(X\)的线性子空间,则 \[ \inf_{y\in Y}\lVert x-y\rVert =\max_{l\in X^*_Y,\lVert l\rVert =1}|l(x)|. \] Remark 在原文中的约束是\(\lVert l\rVert \leq 1\),不难看出约束可以改写成\(\lVert l\rVert =1\)。
Theorem 12(原文Ch 8 Thm 7') 设\(Y\)是\(X\)的线性子空间,对任一\(l\in X^*\),定义 \[ \lVert l\rVert _Y:=\sup_{y\in Y,\lVert y\rVert =1}|{l(y)}|, \] 则 \[ \lVert l\rVert _Y=\min_{m\in X^*_Y}\lVert l-m\rVert . \] Theorem 13(原文Ch 8 Thm 18) 设\(K\)是\(X\)的闭凸子集,\(z\)是\(X\)中不属于\(K\)一点,则 \[ \inf_{y\in K}\lVert z-y\rVert =\sup_{\lVert l\rVert =1}[l(z)-S_K(l)]. \]
Theorem 11的几何意义
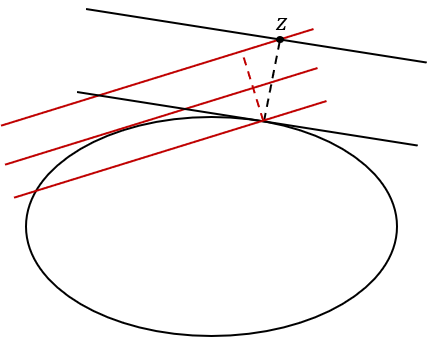
\(l\in X^*_Y\)意味着\(Y\)是超平面\(P(l,0)\)的子空间,即超平面\(P(l,c)\)总是与\(Y\)“平行”(指的是\(Y\)总能沿着一个方向平移后到\(P(l,c)\)中,即存在\(z\in X\)使得\((Y+z)\subset P(l,c)\)。那么,\(Y\)上任意一点到超平面\(P(l,l(x))\)的距离都相同。又由于\({\bf{0}}\in Y\),\(Y\)到\(P(l,l(x))\)的距离总是\(|l(x)|\)。而\(x\)在超平面\(P(l,l(x))\)上,因此\(x\)到\(Y\)的距离一定大于等于\(|l(x)|\)。
正如上图所示,取遍\(l\in X^*_Y\)且\(\lVert l\rVert =1\)的\(l\),就是考虑零空间包含\(Y\)的\(l\)(即零空间在“绕\(Y\)旋转”)。根据之前的讨论,\(P(l,l(x))\)上总有一个向量\(z\)到原点的距离最短,此时\(\lVert z\rVert\)就是\(Y\)到\(P(l,l(x))\)的距离,\(Y+z\)就是\(Y\)在\(P(l,l(x))\)上的垂直投影。
当\(P(l,0)\)“绕着\(Y\)旋转”时,\(P(l,l(x))\)也在“绕着\(Y+x\)旋转”,\(Y+z\)也在\(P(l,l(x))\)上移动,直到移动到\(x\)上,就取到了“过\(x\)与\(Y\)平行的超平面”中距离\(Y\)最远的一个,此时的距离即\(x\)到\(Y\)的距离。
Theorem 12的几何意义
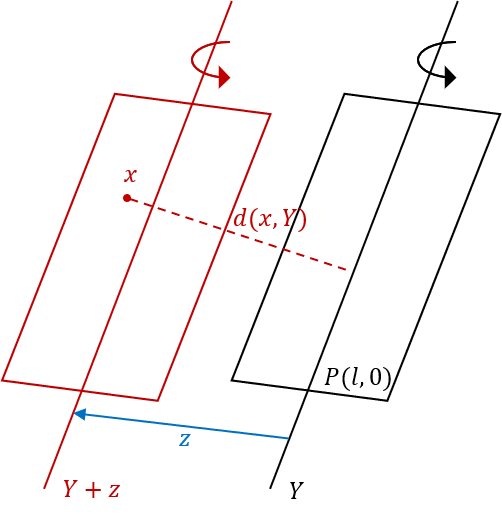
首先要注意到一点,\(\{l-m\colon m\in X^*_Y\}=\{l'\in X^*\colon l'|_Y=l|_Y\}\)。先来分析\(l'|_Y=l|_Y\)的含义。
设\(B_Y\)为\(Y\)上的单位球,和之前的讨论一样,注意到\(\overline H(l,S_{B_Y}(l))\)(下面简写为\(H\))是\(B_Y\)的支撑半平面。任取\(y\in Y\),一定存在唯一的常数\(c(l,y)\in\R\),使得\(c(l,y)y\in H\),即\(c(l,y)\)是伸缩\(y\)使得\(y\)落在支撑半平面上的系数。
不妨称其为\(Y\cap H\)为\(Y\)与\(H\)的超交线。由于\(l'\)和\(l\)限制在\(Y\)上相等,则\(S_{B_Y}(l)=S_{B_Y}(l')\)。不妨设\(l'\)导出的\(B_Y\)上的支撑半平面为\(H'\),则\((Y\cap H)=(Y\cap H')\),即\(Y\)与\(H\)和\(H'\)的超交线相同。很显然,如果\(l\)和\(l'\)在\(B_Y\)上的支撑半平面分别是\(H\)和\(H'\),则\(Y\)在\(H\)和\(H'\)上的超交线相同也能推出\(l|_Y=l'|_Y\)。
另外,还要注意到一点。设原点到\(l\)在\(X\)的单位球的支撑半平面和\(Y\)的单位球的支撑半平面的距离分别为\(D\)和\(D_Y\),则有 \[ \frac{\lVert l\rVert }{\lVert l\rVert _Y}=\frac{D}{D_Y}, \]
很显然有\(D\geq D_Y\),Theorem 12的几何意义是取遍\(H'\)与\(Y\)交线和\(H\)与\(Y\)交线相同的\(l'\),直到取到在\(X\)上单位球的支撑半平面和\(Y\)上的支撑半平面相同的\(l'\),该\(l'\)就满足\(\lVert l' \rVert=\lVert l' \rVert_Y\)。

上图把这些内容可视化了。(A)中蓝色平面是\(l\)在\(B_Y\)上的支撑半平面,黄色平面是\(l\)在\(X\)的单位球上的支撑半平面,超交线退化成\(Y\)和蓝色平面的交点\(Y'\)。(B)是侧视图,红色平面对应的\(l'\)即满足\(\lVert l' \rVert=\lVert l' \rVert_Y\)的\(l'\)。
Theorem 13的几何意义
令\(U=\{l\in X^*\colon \lVert l\rVert =1,l(z)-S_K(l)\geq0\}\),根据超平面分离定理\(U\neq\emptyset\),因此我们只需考虑\(U\)中的\(l\)。此时,\(l(z)-S_K(l)\)即超平面\(P(l,l(z))\)和\(P(l,S_K(l))\)的距离。这个定理说的是\(z\)到\(K\)的(由\(U\)中的泛函导出)支撑半平面\(H\)的距离和\(z\)到\(K\)的距离的关系。具体可以类似前面的讨论结合下图分析,这里不再赘述。