二分图匹配和最大流是非常基础的内容，二分图匹配可以通过重新建图用最大流的算法解决，并且二分图匹配的König定理和最大流的最大流最小割定理形式上相似。在算法竞赛的书籍中，通常都是通过图论的一些技巧来分别证明这两个定理，非常巧妙但总感觉未能涉及本质。因此我打算利用对偶理论对二分图匹配和最大流中的“最大最小”进行讨论。 \[\require{mathtools}\]

一、简析对偶理论

König定理：一张二分图的最大匹配数等于最小点覆盖数。
最大流最小割定理：一个流网络的最大流等于最小割。

对比这两个定理不难发现其共同点：两个问题分别是最大化问题和最小化问题，且最优解的值相等(这里说的是最优解的值，在二分图中连讨论的对象都不同，很显然解也不会相同，但它们之间并非是毫无联系的)。接下来先引入对偶问题的概念，通过这个概念很直观的就能看出两个定理背后的本质。

Definition 1 设$A$为$n\times m$矩阵、$x$为$n\times1$向量、$c$为$1\times n$向量、$y$为$1\times m$向量、$b$为$m\times 1$向量，原问题为： \[ \begin{align*} \max\text{ }&z=cx\\ s.t.\text{ }&Ax\leq b,\\ &x\geq 0.\end{align*}\tag{1}\label{1} \] 则其对偶问题为： \[ \begin{align*} \min\text{ }&w=yb\\ s.t.\text{ }&yA\geq c,\\ &y\geq 0.\end{align*}\tag{2}\label{2} \] 接着来介绍对偶问题中与本文内容比较相关的几个性质：

Theorem 1(弱对偶性) 设$\hat{x},\hat{y}$分别是原问题$\eqref{1}$与其对偶问题$\eqref{2}$的可行解，则$c\hat{x}\leq yb$。

Proof 由(1)，有$A\hat{x}\leq b$，且$\hat{y}\geq 0$，则$\hat{y}A\hat{x}\leq\hat{y}b$，
由(2)，有$yA\geq c$，且$\hat{x}\geq0$，则$\hat{y}A^{T}\hat{x}\geq cx$，从而$c\hat{x}\leq yb$。 $\Box$

Theorem 2(最优性) 设$\hat{x},\hat{y}$分别是原问题$\eqref{1}$与其对偶问题$\eqref{2}$的可行解，且$c\hat{x}=\hat{y}b$，则它们分别是两个问题的最优解。

Proof 设$x^*$是$\eqref{1}$的最优解，则$\hat{y}b=c\hat{x}\leq cx^*$，又由弱对偶性，$cx^*\leq\hat{y}b$，则$cx^*=\hat{y}b=c\hat{x}$。 $\Box$

以及最重要的一个性质：

Theorem 3(强对偶性) 原问题与对偶问题其中一个有最优解，则另一个也有最优解，且最优解的值相等。

这个性质的表述就和上文总结的两条定理的共性很相似了，因此不妨从对偶理论的角度来考虑它们。

二、网络流中的对偶问题

算法导论中，网络流$G=(V,E,c)$的最大流问题的数学模型可以如下表示： \[ \begin{align*} \max\text{ }&\sum_{v\in V}[f(s,v)-f(v,s)]\\ s.t.\text{ }&0\leq f(u,v)\leq c(u,v),\forall u,v\in V,\\ &\sum_{v\in V}f(u,v)=\sum_{v\in V} f(v,u),\forall u\in V\backslash\{s,t\}.\end{align*} \] 从边的角度考虑似乎不太能写出它的对偶问题，因此我们重构一下模型，令$P$是$G=(V,E,c)$中所有$s$到$t$的简单路径的集合，$f_p$是路径$p$上的流量，则可写出如下数学模型： \[ \begin{align*} \max\text{ }&\sum_{p\in P}f_p\\ s.t.\text{ }&\sum_{p\in\{x\in P|e\in x\}}f_p\leq c(e),\forall e\in E,\\ &f_p\geq0,\forall p\in P.\end{align*}\tag{3}\label{3} \]

不难看出，每条边对应一个限制条件，$\eqref{1}$中的向量$b$在这里即是容量上限$c$，系数矩阵中$(i,j)$元为$1$当且仅当第$i$条边在第$j$条路径上，否则为$0$。则不难写出其对偶问题的数学模型： \[ \begin{align*} \min\text{ }&\sum_{e\in E}c(e)y(e)\\ s.t.\text{ }&\sum_{e\in P} y(e)\geq 1,\forall p\in P,\\ &y(e)\geq 0,\forall e\in E.\end{align*}\tag{4}\label{4} \] 如果将$y$的取值限制在$\{0,1\}$上，不难看出问题中每条路径上至少有一条边取值为$1$，这就说明取出所有取值为$1$的边就是一个分割。而目标是所有取值为$1$的边的权值和最小，即该分割的权值和最小，就可以看出这是最小割问题。

例如下图：

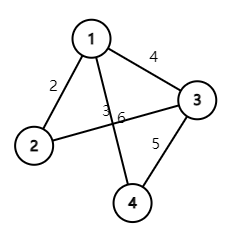
用$\eqref{3}$式的表述，对这个网络，有$P=\{\{(1,2),(2,3),(3,4)\},\{(1,3),(3,4)\},\{(1,4)\}\}$，最大流问题可表示为： \[ \begin{align*} &\max\sum_{p\in P}f_p\\ s.t.\text{ }&\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ 1&0&0\\ 1&1&0 \end{pmatrix}\begin{pmatrix}f_{p_1}\\f_{p_2}\\f_{p_3}\end{pmatrix} \leq \begin{pmatrix} 2\\ 4\\ 3\\ 6\\ 5 \end{pmatrix},\\ &f_{p_1},f_{p_2},f_{p_3}\geq0.\end{align*} \] 其对偶问题为： \[ \begin{align*} &\min (y_1,y_2,y_3,y_4,y_5)\begin{pmatrix} 2\\4\\3\\6\\5\end{pmatrix}\\ s.t.\text{ }&(y_1,y_2,y_3,y_4,y_5)\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&1\\ 1&0&0\\ 1&1&0 \end{pmatrix}\geq\begin{pmatrix} 1\\1\\1\end{pmatrix},\\ &y_1,y_2,y_3,y_4,y_5\geq0.\end{align*} \] 通过这个例子很清晰的就能看出两者之间的联系。

接着，只需要证明$\eqref{4}$有取值在$\{0,1\}$上的最优解即可。

Proof 设$\hat{y}$是一个最优解，显然$\forall e\in E,0\leq\hat{y}(e)\leq 1$。若$\exists e'\in E,0<\hat{y}(e')<1$，设$P'=\{p\in P|e'\in p\}$，
任取$P'$中的一条路径$p$，一定还存在除了$e'$之外的边满足$\hat{y}$值大于$0$，每条路径中都取出这样的一条边，构成一个边集$E'$。
假设$\sum_{e\in E'}c(e)>c(e')$，设$e_0\in\text{argmax}_{e\in E'}(c(e))$，考虑如下解： \[ y^*(e)\coloneqq\begin{cases} \hat{y}(e)-\hat{y}(e_0)&\text{if $e\in E'$,}\\ \hat{y}(e)+\hat{y}(e_0)&\text{if $e=e'$,}\\ \hat{y}(e)&\text{else.} \end{cases} \] 则有
\[ \begin{align*} \sum_{e\in E}c(e)y^*(e)&=\sum_{e\in E\backslash({E'}\cup\{e'\}}c(e)\hat{y}(e)+\sum_{e\in E'}c(e)(\hat{y}(e)-\hat{y}(e_0))+c(e')(\hat{y}(e')+\hat{y}(e_0))\\ &=\sum_{e\in E}c(e)\hat{y}(e)+(c(e')-\sum_{e\in E'}c(e))\hat{y}(e_0)\\ &<\sum_{e\in E}c(e)\hat{y}(e). \end{align*} \] 这与$\hat{y}$为最优解矛盾，因此$\sum_{e\in E'}c(e)\leq c(e')$。同理可得$\sum_{e\in E'}c(e)\geq c(e')$，从而$\sum_{e\in E'}c(e)=c(e')$。
那么考虑如下解： \[ \overline{y}\coloneqq\begin{cases} \hat{y}(e)+\hat{y}(e')&\text{if $e\in E'$,}\\ 0&\text{if $e=e'$,}\\ \hat{y}(e)&\text{else.} \end{cases} \] 很显然$\sum_{e\in E}c(e)\bar{y}(e)=\sum_{e\in E}c(e)\hat{y}(e)$，即$\bar{y}$也是最优解。
每进行一次上述的转化，满足$y$值在$(0,1)$上的边的数量至少减少一条，因此进行有限次转化，即可使得所有边的$y$值都大于等于$1$，又由所有$y$值一定小于等于$1$，因此这个解的取值就在$\{0,1\}$上了，所以一定存在一个取值在$\{0,1\}$上的最优解。 $\Box$

因此，结合强对偶性，一个网络上最小割等于最大流。

三、二分图匹配中的最大最小

事实上，我们可以直接用最大流最小割定理导出König定理，考虑图$G=(V=\{A,B\},E)$满足$\forall u,v\in A,(u,v)\notin E,\forall u,v\in B,(u,v)\notin E$，构建源点$s$与汇点$t$，将$s$与$A$中所有点连边、$t$与$B$中所有点连边，所有边的容量设为$1$，得到网络$G'=(V,E,c)$，不加证明地给出如下引理：

Lemma 1 任取$G$中的一个点覆盖$V'=A'\cup B',A'\subset A,B'\subset B$，则$[\{s\}\cup A',\{t\}\cup B']$是$G'$的一个切割，且包含了$G'$的所有切割，即$G$的点覆盖与$G'$的切割构成一个双射。

利用匈牙利树可以轻松地证明这个引理，再利用最大流最小割定理即可证明König定理，这里不再赘述。让我们再从线性规划的角度来考虑，对于按上述定义的图$G$，最大匹配数学模型为： \[ \begin{align*} \max\text{ }&\sum_{e\in E}x(e)\\ s.t.\text{ }&\sum_{e\in E\wedge v\in e}x(e)\leq 1,\forall v\in V,\\ &x(e)\geq0,\forall e\in E.\end{align*} \] 再写出它的对偶问题： \[ \begin{align*} \min\text{ }&\sum_{v\in V}y(v)\\ s.t.\text{ }&y(u)+y(v)\geq1,\forall (u,v)\in E,\\ &y(v)\geq 0,\forall v\in V.\end{align*}\tag{5}\label{5} \] 类似对最小割问题的证明，这两个问题再二分图上也一定都存在取值在$\{0,1\}$上的最优解。

接着来考虑最大独立集，二分图上最大独立集的数学模型为： \[ \begin{align*} \max\text{ }&\sum_{v\in V} z(v)\\ s.t.\text{ }&z(u)+z(v)\leq 1,\forall (u,v)\in E,\\ &z(v)\in\{0,1\},\forall v\in V.\end{align*}\tag{6}\label{6} \] 做一个变换$w(v)=1-z(v)$，则就$\eqref{6}$变成了： \[ \begin{align*} \min\text{ }&|V|-\sum_{v\in V}w(v)\\ s.t.\text{ }&w(u)+w(v)\geq1,\forall(u,v)\in E,\\ &w(v)\in\{0,1\},\forall v\in V.\end{align*}\tag{7}\label{7} \] 不难看出，$\eqref{7}$的最优解正是$\eqref{5}$的一个取值在$\{0,1\}$上的最优解，即最小点覆盖=$|V|$-最大独立集。

比起一个个独立的图论证明，线性规划的证明更加清晰地展现出了它们之间的联系。